Von Schutzmasken und anderen Dilemmata

By Marc Pouly und Eckart Zitzler

Weshalb ziehen so wenige Leute Schutzmasken an? Marc Pouly, Studiengangleiter Master of Science in Engineering und Eckart Zitzler, Vizedirektor und Leiter Forschung am Departement Informatik, begeben sich auf Spurensuche und ergründen das Dilemma aus spieltheoretischer Sicht.

Nach dem Lockdown

Seit dem 8. Juni 2020 ist die Hochschule Luzern wieder für Studierende und Mitarbeitende unter Einhaltung der gängigen Sicherheitsregeln geöffnet. Aufgrund der niedrigen Ansteckungsraten waren weitreichende Lockerungen möglich.

Die Informatik hat Wissenschaftlerinnen und Wissenschaftlern geholfen, über Modellrechnungen in die Zukunft zu schauen, die Ausbreitung des Virus zu antizipieren und Schutzmassnahmen abzuleiten. Gebannt ist die Gefahr allerdings nicht: Fachleute und Vertreter der Regierung warnen vor einer zweiten Welle. Auch hier kann die Informatik einen Beitrag leisten, dieses Szenario bestmöglich zu verhindern. Contact-Tracing-Apps können die Kontakte einer infizierten Person rückverfolgen und helfen, die Ausbreitung des Virus mit Quarantänemassnahmen einzudämmen.

Was braucht es, damit Schutzmassnahmen umgesetzt werden? Die Methoden der Informatik helfen bei der Suche nach Lösungen

Weiter empfehlen öffentliche Verkehrsbetriebe das Tragen von Schutzmasken in Bus, Tram und Bahn, wenn der Sicherheitsabstand von zwei Metern nicht eingehalten werden kann. Doch welcher Voraussetzungen bedarf es eigentlich, damit solche Schutzmassnahmen umgesetzt werden? Ein weiterer Fall, für den die Methoden der Informatik Erklärungsansätze bieten und bei der Suche nach Lösungen unterstützen können.

Alice und Bob und die Maske im ÖV

Die Pendlerin Alice und der Pendler Bob treffen sich im Zug. Wie in der folgenden Abbildung skizziert, gibt es nun vier mögliche Situationen: Beide tragen eine Schutzmaske, niemand trägt eine Schutzmaske, oder es trägt entweder Alice oder Bob eine Schutzmaske.

Über die Wirksamkeit von Schutzmasken wurde in den letzten Wochen viel debattiert. Ob Alice und Bob eine Maske tragen, hängt jedoch nicht von wissenschaftlicher Evidenz, sondern von ihren subjektiven Überzeugungen ab.

Nehmen wir einmal an, dass beide Protagonisten – zum Beispiel aufgrund eines Zeitungsberichts – zur Überzeugung gelangen, dass Schutzmasken das Ansteckungsrisiko der Trägerin oder des Trägers signifikant senken. Folglich ist es für Alice vorteilhaft, wenn sie selbst eine Maske trägt, unabhängig davon, wie sich Bob entscheidet. Wenn wir weiter annehmen, dass es Alice ebenfalls lieber ist, wenn Bob eine Maske trägt, lässt sich folgende Reihenfolge der obigen Situationen als Präferenz von Alice ableiten.

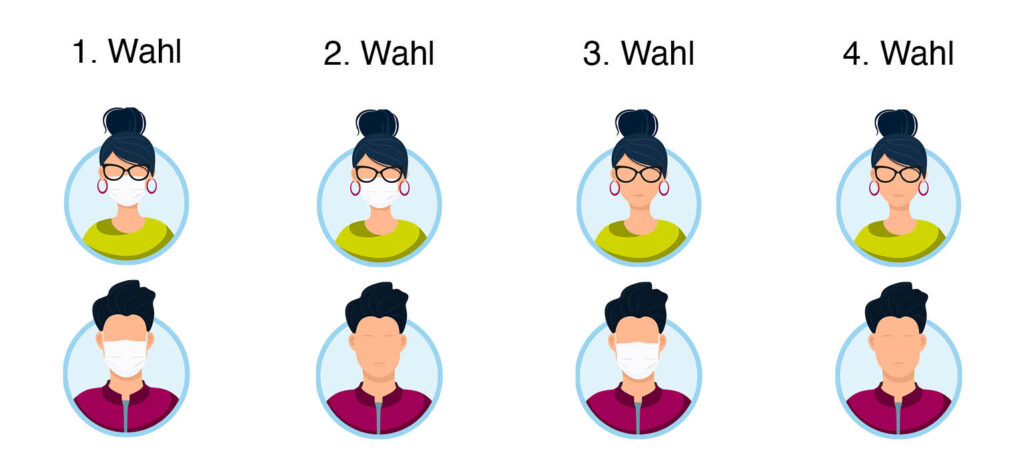
Aus Bobs Perspektive ergibt sich symmetrisch die nachfolgende Reihenfolge als Präferenz:

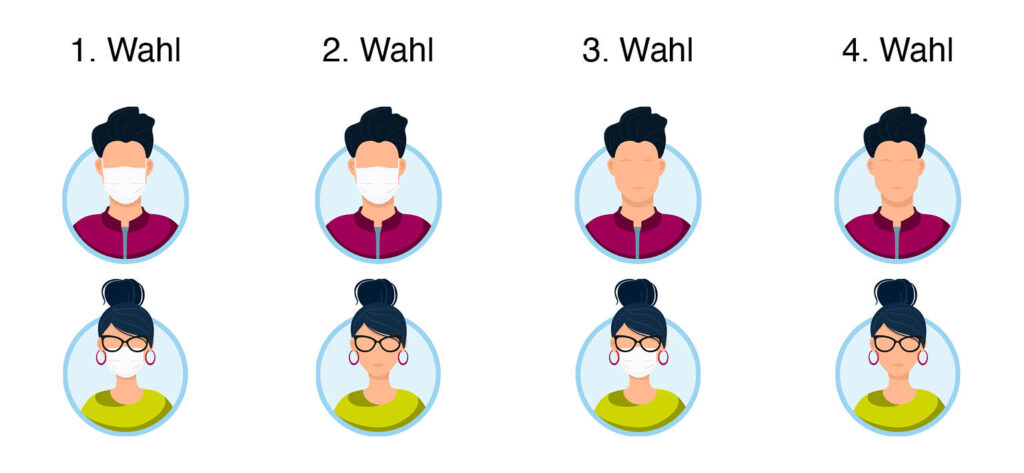
Dies ist nur eine Präferenzreihenfolge, welche mit der Annahme konsistent ist, dass Schutzmasken das Ansteckungsrisiko der Trägerin oder des Trägers senken –  es gibt deren weitere fünf Varianten. Eine spieltheoretische Analyse ergibt in allen Fällen das gleiche Resultat und bestätigt unser intuitives Verständnis: Entscheiden Alice und Bob unabhängig und ohne Wissen voneinander im Glauben, dass Schutzmasken den Träger vor einer Virusinfektion schützen, dann werden sie beide eine Maske tragen.

Wer dieser Tage mit Zug, Bus oder Tram unterwegs ist, wird jedoch festgestellt haben, dass nur sehr wenige Menschen tatsächlich eine Schutzmaske tragen. Oder wie SRF titelt: «Masken tragen in Zug und Bus – fast niemand hält sich an die Empfehlung». Die Voraussage der Spieltheorie scheint hier also nicht unseren Beobachtungen im Alltag zu entsprechen.

Was wir glauben, entscheidet das Spiel

Ändern wir nun unsere Annahmen: Alice und Bob glauben, dass sie mit dem Tragen einer Maske grundsätzlich nur die anderen vor einer Infektion schützen. Auch diese Überzeugung ist nachvollziehbar, hat doch Daniel Koch vom Bundesamt für Gesundheit im März und April 2020 verschiedentlich erklärt, dass (für die breite Bevölkerung erhältliche) Masken nur einen Nutzen hätten, wenn der Träger oder die Trägerin selbst krank sei – einen Schutz vor Ansteckung gebe es damit nicht. Nehmen wir weiter an, dass unsere Pendler sich gesund fühlen und keine Corona-Symptome aufweisen. Schliesslich gehen wir davon aus, dass Alice und Bob das Tragen einer Schutzmaske als unkomfortabel empfinden, eine Annahme, die wohl die wenigsten Leserinnen und Leser infrage stellen werden.

Welcher Situation wird Alice nun den Vorzug geben? Da sie nichts über Bobs Befindlichkeit weiss, wird sie es in jedem Fall vorziehen, dass Bob eine Maske trägt. Gleichzeitig sieht Alice keinen Anlass, durch das Tragen einer unbequemen Schutzmaske Bob vor einer Infektion schützen zu müssen – sie fühlt sich ja gesund. Die Reihenfolge ihrer Präferenzen sieht nun wie folgt aus:

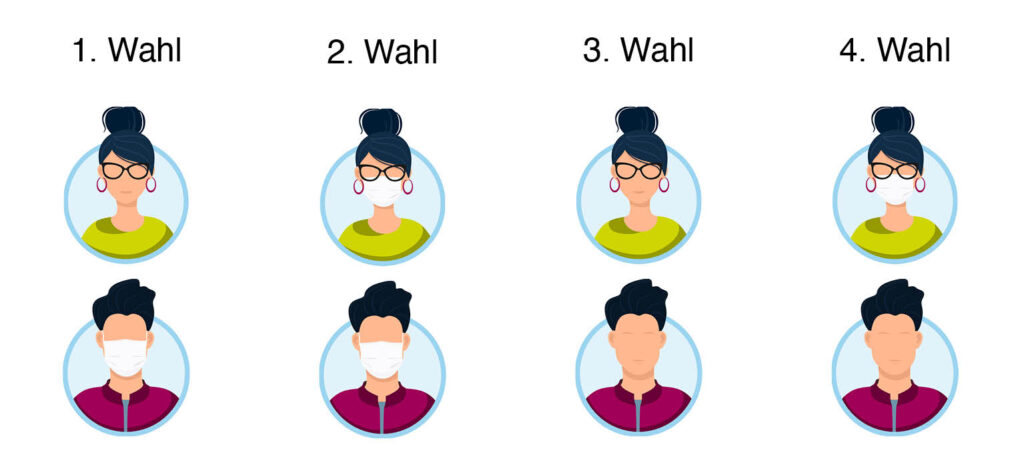
Analog ergibt sich für Bob diese Reihenfolge:

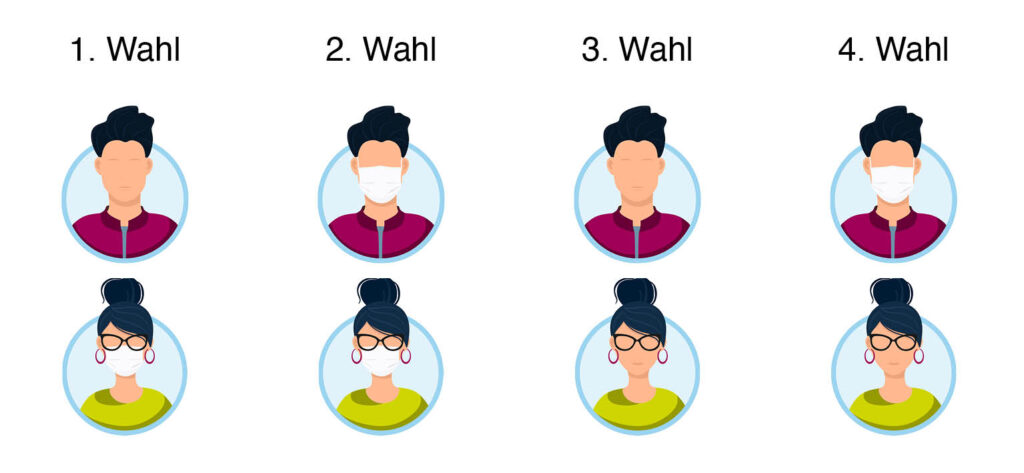
Was hat sich nun in der Präferenzreihenfolge verändert? Jetzt ist es so, dass beide Protagonisten das generelle Tragen von Schutzmasken als zweitbeste Lösung einstufen. Trotzdem handelt es sich dabei immer noch um eine sogenannte Pareto-optimale Lösung: Keine Partei könnte die Situation für sich verbessern, ohne sie für die andere Partei zu verschlechtern. Aus übergeordneter Sicht der Gesellschaft wäre das generelle Tragen von Masken also tatsächlich immer noch die erstrebenswerteste Lösung. Aber wie erklärt sich dann unsere Beobachtung, dass praktisch niemand im ÖV eine Schutzmaske trägt, also die folgende Situation auftritt?

Dies liegt daran, dass sich unsere zwei Pendler mit hoher Wahrscheinlichkeit nicht näher kennen und damit die Entscheidung, ob sie eine Schutzmaske tragen oder mit sich führen wollen, unabhängig voneinander treffen.

Der rationale Agent

Im Jargon der Informatik sind Alice und Bob rationale Agenten. Dabei bedeutet rational, dass, sie immer die vorteilhaftere Möglichkeit in Bezug auf ihre eigenen Präferenzen wählen, wenn sie sich zwischen zwei Varianten entscheiden müssen:

Niemand wählt absichtlich schlecht!

Wie also wird sich Alice entscheiden?

Angenommen Bob trägt eine Maske. Zieht Alice keine Maske an, so erreicht sie damit ihre erste Wahl. Trägt sie hingegen auch eine Maske, so ist das nur ihre zweite Wahl. Also wird Alice keine Maske anziehen – wozu auch? Sie selbst ist durch Bob geschützt, und da sie sich gesund fühlt, wählt sie die für sich angenehmere Variante.

Angenommen Bob trägt keine Maske. Zieht Alice eine Maske an, erreicht sie ihre vierte und letzte Präferenz. Zieht sie hingegen keine Maske an, so ist die resultierende Situation immerhin ihre dritte Präferenz. Folglich wird Alice keine Maske anziehen – denn sie hat daraus keinen Vorteil, fühlt sich gesund und würde nur den Nachteil des eingeschränkten Komforts einfahren.

Auf eine Maske zu verzichten ist immer die bessere Option in Bezug auf die individuellen Präferenzen.

Zusammenfassend gilt: Egal wie sich Bob entscheidet, auf eine Maske zu verzichten ist immer die bessere Option für Alice in Bezug auf ihre individuellen Präferenzen. Aufgrund der symmetrischen Präferenzreihenfolge gilt die gleiche Aussage für Bob. Auf eine Schutzmaske zu verzichten ist eine dominante Strategie und damit immer die beste Reaktion auf die vom anderen Pendler gewählte Strategie. Zu Ehren des 2015 verstorbenen Mathematikers John Nash, der für seine Pionierleistung auf dem Gebiet der Spieltheorie 1994 den Nobelpreis verliehen bekam, wird dieser Zustand als Nash-Equilibrium (Nash-Gleichgewicht) bezeichnet.

Sowohl für Alice wie auch für Bob würde das generelle Tragen von Masken – die Situation, in der beide eine Maske tragen – eine bessere Option darstellen als das Nash-Equilibrium – die Situation, in der weder Alice noch Bob eine Maske tragen –, welche sich aufgrund des rationalen Verhaltens beider Parteien einstellen wird. Nehmen wir also an, Alice und Bob würden sich ohne Schutzmasken im ÖV gegenübersitzen. Nun kommt eine Drittperson dazu und bietet Alice eine Schutzmaske an – wird sie die Maske anziehen? Nein, denn die Situation, dass nur sie eine Maske trägt, stellt für Alice eine schlechtere Situation dar als diejenige, in der beide keine Maske tragen. Dasselbe gilt für Bob. In einem Nash-Equilibrium ist keine Partei gewillt, unilateral von ihrer gewählten Strategie abzuweichen. Oder wie es der Yale-Professor Ben Pollack einmal ausdrückte:

Rational choice sometimes leads to outcomes that suck!

Übrigens lassen sich aus obiger Annahme wiederum fünf weitere konsistente Präferenzreihenfolgen ableiten. Die spieltheoretische Analyse führt in allen Fällen zum exakt gleichen Resultat mit der Situation, dass beide keine Masken tragen, als einzigem Nash-Equilibrium.

Gefangen im Dilemma

Und nun? Dieses Szenario ist in der Fachwelt als Gefangenendilemma bekannt: Wir entscheiden als Individuen unabhängig und gesteuert durch subjektive Präferenzen, woraus sich später das gesellschaftliche Verhalten ergibt. Und was individuell gut ist, kann über alle Individuen betrachtet schlecht sein. In diesem Modell gibt es tatsächlich nur einen Ausweg: Alice und Bob müssten zur Überzeugung gebracht werden, dass der Verzicht auf eine Schutzmaske einen schwerwiegenden Nachteil mit sich bringt. Wenn sie meinen, dass sie sich mit Masken selbst schützen können, ergibt sich, so haben wir gesehen, das gewünschte Resultat. Wenn sie davon nicht überzeugt sind, hilft als letzter Ausweg aus dem Dilemma nur eine Maskenpflicht unter Strafandrohung. Denn nicht wissenschaftliche Evidenz, sondern persönlicher Glaube und Überzeugungen bestimmen, in welcher Reihenfolge Alice und Bob die vier eingangs beschriebenen Situationen präferieren.

Wir entscheiden als Individuen unabhängig und gesteuert durch subjektive Präferenzen, woraus sich später das gesellschaftliche Verhalten ergibt.

Natürlich haben solche Modelle ihre Grenzen, wenn es darum geht, soziale Phänomene zu erklären. Wir bewegen uns ja in einem öffentlichen Raum mit vielen Menschen und unterliegen weiteren Einflussfaktoren wie zum Beispiel sozialem Druck: Je mehr Menschen eine Maske tragen, desto grösser ist der soziale Druck, ebenfalls eine zu tragen. Beim oben erwähnten (äquivalenten) Gefangenendilemma liess der amerikanische Professor Robert Axelrod bereits in den 1980er-Jahren verschiedene Verhaltensstrategien gegeneinander antreten und simulierte auf einem Computer die Evolution. Der Gewinner war die Strategie Tit for Tat («Wie du mir, so ich dir»): Beim ersten Mal kooperiert Alice und trägt eine Maske; bei allen darauffolgenden Begegnungen tut Alice genau das, was ihr Gegenüber bei der letzten Begegnung getan hat.

Wo Spieltheorie sonst noch zum Einsatz kommt

Spieltheoretische Modelle kommen in der Informatik und insbesondere in der Künstlichen Intelligenz immer dann zum Einsatz, wenn sich kompetitive Situationen ergeben;  etwa dann, wenn eine Aktion eines Computerprogramms das Ergebnis eines anderen Programms beeinflusst und es keine globale Koordination oder Steuerung der einzelnen Aktionen gibt. Beispiele dafür sind der automatisierte Wertpapier- oder Energiehandel, Auktionssysteme für den Zugriff auf kritische Ressourcen, Google AdWords, die automatisierte Festlegung von Preisen auf Buchungsplattformen oder die formale Verifikation von Sicherheitsprotokollen.